N.B.: There is a serious mistake in the calculus below, see why.
Reading Ludwig Wittgenstein’s Tractatus Logico-Philosophicus (in English), I discovered an astonishing thing about what’s wrong with outliners. As you may know (and if you don’t, get it and read it), the TLP is arranged as a hierarchy of sentences, and their position is given by a decimal number. For example, the first few entries are numbered like this:
1
1.1
1.11
1.12
1.13
1.2
1.21
Which obviously corresponds to an outline like
1
1.1
1.11
1.12
1.13
1.2
1.21
So far, so good. As the description says,
The sentences n.1, n.2, n.3, etc. are remarks at sentence n; the sentences n.m1, n.m2, etc. remark at sentence n.m; and so on.
If we wanted to determine an abstract data type for outlines, it would look like this (say, in Standard ML):
This is just a plain old tree with any amount of children. In fact, this is what most (all?) outliners and file formats use: consider OPML, XOXO, Emacs outline/org-mode,… All outliners should be able to create outlines like this.
As a matter of fact, note that each decimal is nested according to its length.
Let’s continue reading TLP, and a bit later, we find:
2.02
2.0201
2.021
2.0211
2.0212
2.022
2.023
2.0231
At first, I thought the typesetter maybe confused something there, because what are all all the zeros for? But obviously, there is a deeper meaning of this. Once again, let’s construct a “tree” of this:
2.02
2.0201
2.021
2.0211
2.0212
2.022
2.023
2.0231
It is easy to see that this is not a regular tree. Sometimes, subsequent entries are indented twice! What does this mean? Sentence 2.011 is a remark to 2.01, that is clear. But then, sentence 2.0201 is a remark to sentence 2.020, which is sentence 2.02. Wittgenstein thus found a way to remark on every sentence of the outline and at the same time display closeness and importance of the remark. 2.0201 is less important, but closer to 2.02 than 2.021.
This actually is a great feature for an outliner, because it often is useful to annotate items with remarks in a way that doesn’t reflect the structure of the outline. Say, you restrict the display to certain depths. Then, you’d want to see an overview like
2.02
2.021
2.022
2.023
with no occurrence of 2.0201 because 2.0201 is not important at that level. (Else, it should have been 2.021!)
How can we represent this with classical outliners? An easy option would be to insert an empty node below 2.02 and remark on it. However, this looks ugly and is a hack. (It works okay with Emacs outlines, where you can leave out empty heads.) It doesn’t work that nice with other software or when the outline is rendered as HTML, because of all the empty nodes sticking around.
The datatype (1) is therefore unable to reflect the structure of the TLP. Let’s fix it like explained:
Which allows us to leave nodes empty. Now, this type is kind of unsuitable for at least two reasons. First, empty nodes should appear only as the first child, and not everywhere. And second, empty nodes always should have children.
Let’s try this alternative:
Where the second element is the subtree annotating just the parent node. 2.02 can be represented with this (try it).
But let’s read further:
6
6.001
6.002
6.01
6.02
6.021
6.022
6.03
6.1
You see, this Wittgenstein was a clever guy. This corresponds to the outline:
6
6.001
6.002
6.01
6.02
6.021
6.022
6.03
6.1
And this probably is why the work has decimal numbers, and isn’t printed as an outline…
However, there is a nice way to render outlines like these (and graphical outliners should adapt it):
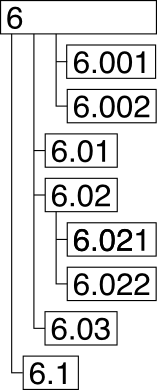
Can type (2) represent this structure? No, because we’d have to provide an item for the parent node of 6.001, but there is none.
Back to the scratch-pad.
This actually is the type of a nested list, and likewise, we can (and will, for the rest of this piece) give the outline as an s-expression:
(6 ((6.001 6.002) 6.01 6.02 (6.021 6.022) 6.03) 6.1)
However, there are more possible s-expressions than outlines, for example:
(1 ((1.01 1.02) (1.03 1.04)))
and
(1 ((1.01 1.02 1.03 1.04)))
are equivalent when interpreted as outline, both represent
1
1.01
1.02
1.03
1.04
Also, for sake of simplicity, let’s consider (1 ((2))) and (1 (2)) to
be equivalent: You cannot remark with less importance on 1 than
anything. (Note that (1 ((2) 3)) and (1 (2 3)) are different!)
Therefore, we can define a outline normal form, which follows by reduction according to these rules:
[Now look closely at these rules! Do you recognize anything? It is the dual to Spencer-Brown’s Laws of Form! Which are reduced by
… but let’s not go deeper into that.]
Enforcing outline normal form as a type is hard, but reducing general
nested lists is easy (the system is
confluent, it’s not),
and every nested list easily reduces to a valid normal form. Writing
a type that allows normal form only is left as an exercise for the
reader. ;-)
Apart from outline normal form, also let’s define fully-parenthesized form, which is generated like this:
This form has the nice effect of being writable with only two
punctuation marks (‘(’ and ‘)’) instead of three, like general s-exprs
(‘(’, ‘)’, and some kind of whitespace to separate list entries.)
I’m currently investigating the use of FPF as external representation for outlines as text files. (“Currently” is a bit of an understatement, because I’ve been there almost four years ago already.)
For sake of completeness, and because the Tractatus actually uses it internally for some formulas, outlines can be represented in Peano’s “dots” notation (see Mark Dominus’ explanation and a few examples by Wolfram (about 80% down)). Roughly,
You always can use a lower precedence if the levels below are not in use (this corresponds to reduction to outline normal form):
The “benefit” of this representation is that you need less symbols, but instead an unlimited amount of different ones.
To summarize: Analyzing the structure of the Tractatus, we found a
style of outline with useful properties that is not supported by
modern outliners. We have found a type for these structures (they are
a kind of s-expression), a graphical representation, a confluent
normal form and a representation that uses a minimal amount of
punctuation.
